18屆上海市嘉定區(qū)高考數(shù)學(xué)模擬試卷
一.填空題(本大題滿分48分)本大題共有12題,只要求直接
填寫結(jié)果���,每個空格填對得4分���,否則一律得零分.
1.函數(shù)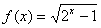 的反函數(shù)是
的反函數(shù)是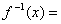 ________________________.
________________________.
2.復(fù)數(shù)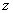 滿足
滿足 ,則
,則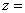 _________.
_________.
3.已知向量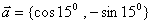 ���,
���,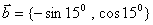 �����,則
�����,則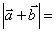 ________.
________.
4.(理)在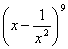 的展開式中����,
的展開式中����,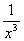 的系數(shù)是__________.
的系數(shù)是__________.
(文)若實數(shù)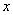 �����,
�����,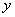 滿足
滿足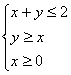 �,則
�,則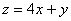 的最大值是_________.
的最大值是_________.
5.若方程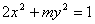 表示焦點在
表示焦點在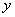 軸上的橢圓,則
軸上的橢圓,則 的取值范圍是______________.
的取值范圍是______________.
6.(理)曲線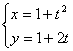 (
(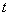 為參數(shù)���,
為參數(shù)���,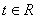 )的焦點坐標(biāo)是_______________.
)的焦點坐標(biāo)是_______________.
(文)曲線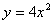 的焦點坐標(biāo)是_______________.
的焦點坐標(biāo)是_______________.
7.(理)已知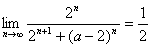 ��,則實數(shù)
��,則實數(shù)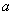 的取值范圍是__________________.
的取值范圍是__________________.
(文)已知數(shù)列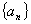 的通項為
的通項為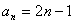 �����,
�����, 是
是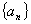 的前
的前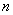 項和�,則
項和�,則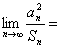 ________.
________.
8.從集合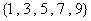 中取出數(shù)
中取出數(shù) ,從集合
,從集合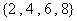 中取出數(shù)
中取出數(shù)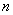 ��,組成分數(shù)
��,組成分數(shù)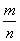 ���,則
���,則
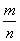 為真分數(shù)的概率是___________.
為真分數(shù)的概率是___________.
9.方程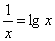 的近似解
的近似解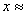 _____________(精確到
_____________(精確到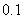 ).
).
10.若點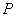 到平面
到平面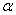 的距離為
的距離為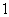 �����,
�����,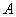 是平面
是平面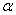 內(nèi)的動點����,斜線段
內(nèi)的動點����,斜線段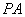 與平面
與平面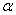 恒成
恒成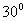 角�,
角�,
則動點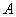 在平面
在平面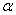 內(nèi)的軌跡所圍成的圖形的面積為_______________.
內(nèi)的軌跡所圍成的圖形的面積為_______________.
11.將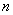 位選民參加無記名投票后的選票進行隨機編號,依次為
位選民參加無記名投票后的選票進行隨機編號,依次為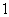 ����,
����,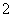 ,…����,
,…����,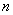 ,參加競選的候選人共有
,參加競選的候選人共有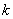 名���,編號依次為
名���,編號依次為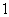 ,
,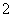 ,…,
,…,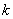 �,給出定義:
�,給出定義:
 �,其中
�,其中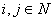 ,且
,且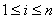 �����,
�����,
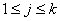 ����,那么
����,那么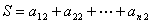 的實際意義是:
的實際意義是:
______________________________________________________________________.
12.(理)已知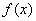 是定義在
是定義在 上的函數(shù),且滿足
上的函數(shù),且滿足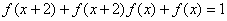 ����,
����,
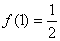 ,
,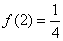 �,則
�,則 ______________.
______________.
(文)已知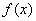 是定義在
是定義在 上的奇函數(shù),且以
上的奇函數(shù),且以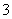 為周期���,若
為周期���,若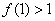 ��,
��,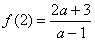 ����,
����,
則實數(shù)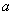 的取值范圍是_______________.
的取值范圍是_______________.
二.選擇題(本大題滿分16分)本大題共有4題,每題都給出
代號為A����、B、C����、D的四個結(jié)論,其中有且只有一個結(jié)論
是正確的��,必須把正確結(jié)論的代號寫在題后的圓括號內(nèi)����,
選對得4分,不選����、選錯或者選出的代號超過一個(不論
是否都寫在圓括號內(nèi)),一律得零分.
13.已知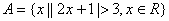 �����,
�����,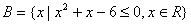 ���,則
���,則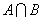 為…( ?�。?/span>
為…( ?�。?/span>
?(A) 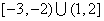 ?(B)
?(B) 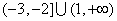 ?(C)
?(C)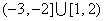 (D)
(D)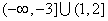
14.在實數(shù)集 上定義運算
上定義運算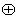 :
: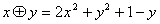 �,則滿足
�,則滿足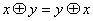 的實數(shù)對
的實數(shù)對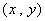 在平面直角坐標(biāo)系內(nèi)對應(yīng)點的軌跡是……………………………………( ?����。?/span>
在平面直角坐標(biāo)系內(nèi)對應(yīng)點的軌跡是……………………………………( ?����。?/span>
(A) 一個圓 (B) 雙曲線 (C) 一條直線 (D) 兩條直線
15.(理)已知函數(shù)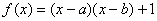 �����,且
�����,且 ��、
��、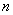 是方程
是方程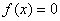 的兩根���,則實數(shù)
的兩根���,則實數(shù)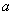 ���、
���、
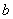 、
、 ��、
��、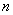 的大小關(guān)系可能是…………………………………………………………( )
的大小關(guān)系可能是…………………………………………………………( )
(A) 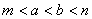 ?(B)
?(B)  ?(C)
?(C) 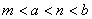 ?(D)
?(D) 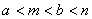
(文)函數(shù)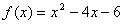 的定義域為
的定義域為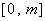 ���,值域為
���,值域為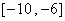 �����,則
�����,則 的取值范
的取值范
圍是……………………………………………………………………………………( ?���。?/span>
(A) 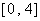 (B)
(B) 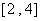 (C)
(C) 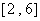 (D)
(D) 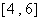
16.(理)一個機器人每一秒鐘前進或后退一步���,程序設(shè)計師讓機器人以前進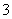 步���,再
步���,再
后退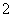 步的規(guī)律移動.如果將機器人放在數(shù)軸的原點,面向正的方向����,以
步的規(guī)律移動.如果將機器人放在數(shù)軸的原點,面向正的方向����,以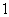 步的距
步的距
離為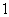 個單位長度.令
個單位長度.令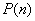 表示第
表示第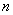 秒時機器人所在位置的坐標(biāo),且記
秒時機器人所在位置的坐標(biāo),且記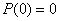 .
.
則下列結(jié)論中錯誤的是………………………………………………………………( ?����。?/span>
(A)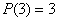 (B)
(B)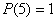 (C)
(C)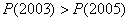 (D)
(D)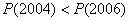
(文)設(shè)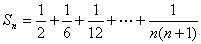 ����,且
����,且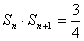 �,則
�,則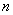 的值是…………( ?����。?/span>
的值是…………( ?����。?/span>
?(A) 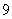 (B)
(B) 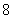 (C)
(C) 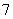 ?(D)
?(D) 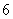
三.解答題(本大題滿分86分)本大題共有6題����,解答下列各題必須寫出必要的步驟.
17.(本題滿分12分)
已知復(fù)數(shù)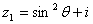 �����,
�����,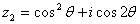 �����,其中
�����,其中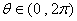 .設(shè)
.設(shè)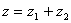 �����,且復(fù)數(shù)
�����,且復(fù)數(shù)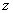 在復(fù)平面上對應(yīng)的點
在復(fù)平面上對應(yīng)的點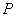 在直線
在直線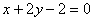 上��,求
上��,求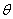 的值所組成的集合.
的值所組成的集合.
18.(本題滿分12分)
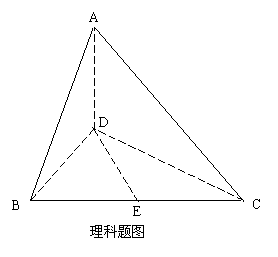
(理)在四面體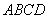 中�,
中�,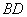 ���、
���、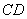 、
、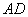 兩兩互相垂直����,且
兩兩互相垂直����,且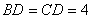 ,
,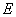 是
是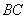 中點��,異面直線
中點��,異面直線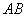 與
與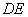 所成角的大小是
所成角的大小是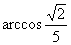 �����,求四面體
�����,求四面體 的體積.
的體積.
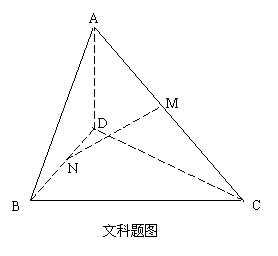 (文)如圖����,在四面體
(文)如圖����,在四面體 中,
中,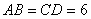 ��,異面直線
��,異面直線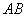 ���、
���、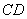 所成角的大小是
所成角的大小是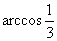 ��,
��,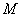 ����、
����、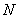 分別是
分別是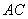 、
、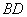 的中點.求線段
的中點.求線段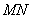 的長.
的長.
19.(本題滿分14分)本題共有2個小題���,第1小題滿分6
分����,第2小題滿分8分.
 某種商品在
某種商品在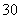 天內(nèi)每件的銷售價格
天內(nèi)每件的銷售價格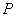 (元)與時間
(元)與時間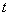 (天)的函數(shù)關(guān)系用下圖中的兩條線段表示��;該商品在
(天)的函數(shù)關(guān)系用下圖中的兩條線段表示��;該商品在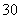 天內(nèi)的日銷售量
天內(nèi)的日銷售量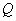 (件)與時間
(件)與時間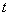 (天)之間的關(guān)系如下表所示:
(天)之間的關(guān)系如下表所示:
?����。?)根據(jù)提供的圖象��,寫出該種商品每件的
銷售價格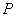 與時間
與時間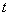 的函數(shù)關(guān)系式����,并根據(jù)表中數(shù)
的函數(shù)關(guān)系式����,并根據(jù)表中數(shù)
據(jù)確定日銷售量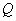 與時間
與時間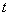 的一個函數(shù)式�����;
的一個函數(shù)式�����;
(2)用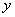 表示該商品的日銷售金額���,寫出
表示該商品的日銷售金額���,寫出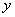
關(guān)于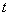 的函數(shù)關(guān)系式�����,求該商品的日銷售金額的最
的函數(shù)關(guān)系式�����,求該商品的日銷售金額的最
大值�����,并指出日銷售金額最大的一天是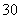 天中的第幾天��?
天中的第幾天��?
20.(本題滿分14分)本題共有2個小題�����,第1題滿分6分����,
第2小題滿分8分.
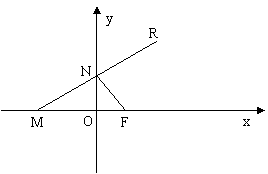
如圖,已知點 �,點
�,點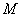 在
在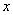 軸上,點
軸上,點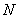 在
在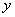 軸上�����,且
軸上�����,且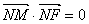 ���,點
���,點 滿足
滿足 .
.
?��。?)求動點 的軌跡
的軌跡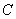 的方程�����;
的方程�����;
?。?)(理)過點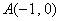 作斜率為
作斜率為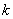 的直線
的直線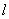 交軌跡
交軌跡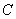 于
于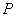 �、
�、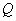 兩點,且
兩點,且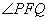 為鈍角����,求直線
為鈍角����,求直線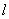 的斜率
的斜率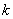 的取值范圍.
的取值范圍.
 (2)(文)過
(2)(文)過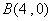 作直線
作直線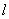 交軌跡
交軌跡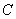 于
于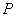 ��、
��、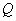 兩點���,求
兩點���,求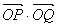 的值.
的值.
21.(本題滿分16分)本題共有3個小題,第1小題滿分4
分����,第2小題滿分5分 , 第3小題滿分7分.
用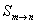 表示數(shù)列
表示數(shù)列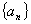 從第
從第 項到第
項到第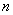 項(共
項(共 項)之和.
項)之和.
(1)在遞增數(shù)列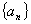 中,
中,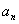 與
與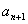 是關(guān)于
是關(guān)于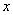 的方程
的方程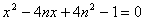 (
(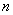 為正整數(shù))的兩個根.求
為正整數(shù))的兩個根.求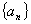 的通項公式并證明
的通項公式并證明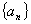 是等差數(shù)列���;
是等差數(shù)列���;
? (2)對(1)中的數(shù)列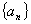 ���,判斷數(shù)列
���,判斷數(shù)列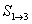 ���,
���,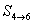 ,
,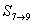 �,…,
�,…,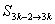 的類型���;
的類型���;
(3)(理)對一般的首項為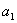 ����,公差為
����,公差為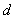 的等差數(shù)列�,提出與(2)類似的問題,你可以得到怎樣的結(jié)論�,證明你的結(jié)論.
的等差數(shù)列�,提出與(2)類似的問題,你可以得到怎樣的結(jié)論�,證明你的結(jié)論.
(3)(文)對(1)中的數(shù)列作進一步研究,提出與(2)類似的問題��,你可以得到怎樣的結(jié)論�����,證明你的結(jié)論.
22.(本題滿分18分)本題共有3個小題��,第1小題滿分5分,
第2小題滿分5分����,第3小題滿分8分.
已知函數(shù)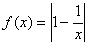 ,
,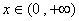 .
.
?���。?)作出函數(shù)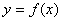 的大致圖象并根據(jù)圖象寫出函數(shù)
的大致圖象并根據(jù)圖象寫出函數(shù)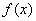 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)(理)證明:當(dāng)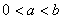 且
且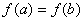 時�,
時�,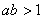 ;
;
?��。?)(文)設(shè)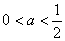 ����,
����,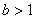 ���,試比較
���,試比較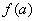 與
與 的大小����;
的大小����;
(3)(理)若存在實數(shù)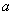 ,
,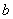 (
(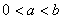 )����,使得函數(shù)
)����,使得函數(shù)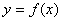 在
在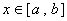 上的函數(shù)的值域為
上的函數(shù)的值域為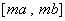 (
(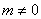 )��,求實數(shù)
)��,求實數(shù) 的取值范圍��;
的取值范圍��;
?(3)(文)是否存在實數(shù)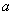 ����,
����,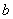 (
(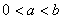 )����,使得函數(shù)
)����,使得函數(shù)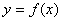 在
在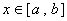 上的值域也是
上的值域也是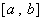 .若存在,求出
.若存在,求出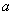 ���,
���,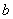 的值���;若不存在,請說明理由.
的值���;若不存在,請說明理由.
2006年嘉定區(qū)高考數(shù)學(xué)模擬試卷參考答案與評分標(biāo)準(zhǔn)
一���、填空題
1.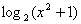 (
(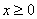 )��;2.
)��;2.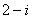 ��;3.1�����;4.(理)
��;3.1�����;4.(理)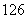 ���;(文)
���;(文)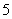 ���;5.
���;5.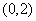 ;
;
6.(理)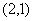 ��;(文)
��;(文)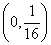 �����;7.(理)
�����;7.(理)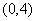 ��;(文)
��;(文)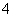 �;8.
�;8. ;9.
;9.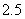 ��;10.
��;10.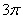 ���;
���;
11.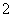 號候選人的得票數(shù)(或同意
號候選人的得票數(shù)(或同意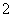 號候選人當(dāng)選的選票數(shù));12.(理)
號候選人當(dāng)選的選票數(shù));12.(理)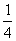 ���;(文)
���;(文)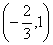 .
.
二���、選擇題
13.A��;14.D���;15.B;16.D
三�、解答題
17.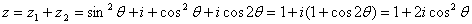 …(4分)
…(4分)
∴ 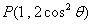 ,∵ 點
,∵ 點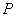 在直線
在直線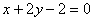 上���,∴
上���,∴  �,…(6分)
�,…(6分)
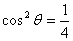 �,
�,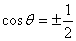 ,…(9分)
,…(9分)
∴ 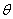 的值所組成的集合是
的值所組成的集合是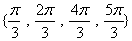 ……(12分)
……(12分)
18(理).取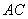 中點
中點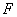 ���,連結(jié)
���,連結(jié)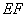 ����、
����、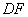 �����,則
�����,則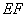 ∥
∥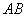 ,
,
∴ 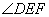 (或其補角)是異面直線
(或其補角)是異面直線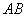 與
與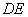 所成的角……(2分)
所成的角……(2分)
設(shè)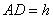 ���,在△
���,在△ 中����,
中����,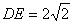 ����,
����,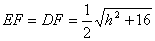 ,……(4分)
,……(4分)
則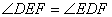 ����,于是
����,于是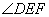 為銳角,
為銳角,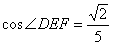 �����,……(6分)
�����,……(6分)
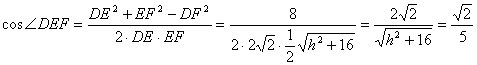
解得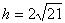 ……(10分)
……(10分)
∴ 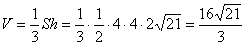 ……(12分)
……(12分)
18(文).取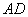 中點
中點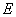 �,連結(jié)
�,連結(jié)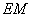 、
、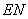 �����,則
�����,則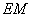 ∥
∥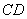 ,
,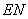 ∥
∥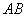 ���,于是
���,于是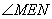 (或
(或
其補角)是異面直線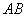 與
與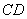 所成的角……(1分)
所成的角……(1分)
當(dāng)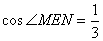 ,則
,則
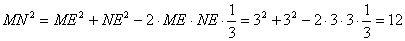 �����,
�����,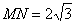 …(6分)
…(6分)
當(dāng)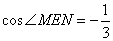 ��,
��,
則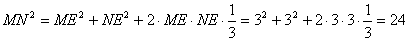 �,
�,
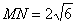 ……………………(11分)
……………………(11分)
∴ 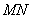 的長為
的長為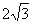 或
或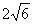 .……(12分)
.……(12分)
19.(1)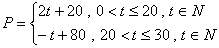 ……(3分)
……(3分)
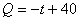 (
(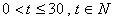 )……(6分)
)……(6分)
(2)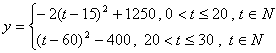 ……(10分)
……(10分)
?當(dāng)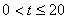 �����,
�����,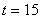 時�,
時�,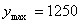 ,當(dāng)
,當(dāng)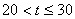 時�,
時�,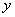 隨
隨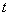 的增大而減小,(12分)
的增大而減小,(12分)
∴ 在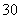 天中的第
天中的第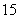 天�,日銷售金額取得最大值
天�,日銷售金額取得最大值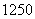 元.…………(14分)
元.…………(14分)
20.(1)由已知,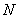 是
是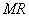 的中點�����,設(shè)
的中點�����,設(shè)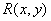 ,則
,則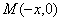 ����,
����,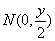 ,……(2分)
,……(2分)
∴ 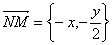 ����,
����,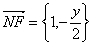 ……(3分),
……(3分),
由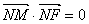 得
得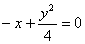 �����,……(4分)即
�����,……(4分)即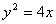 …………(5分)
…………(5分)
∴ 動點 的軌跡方程為
的軌跡方程為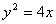 …………(6分)
…………(6分)
(2)(理)直線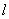 的方程為
的方程為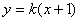 ��,由
��,由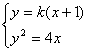 得
得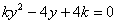 …(8分)
…(8分)
△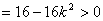 �,
�,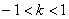 ……(9分),
……(9分),
設(shè)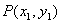 ��,
��,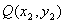 ��,則
��,則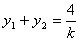 ��,
��,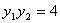 ……(10分)
……(10分)
由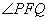 為鈍角�����,可得
為鈍角�����,可得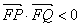 ……(11分)
……(11分)
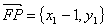 ,
,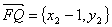 ����,于是
����,于是 ,
,
即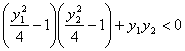 ���,
���,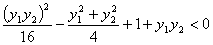 ,
,
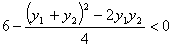 ���,
���,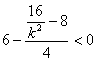 �����,解得
�����,解得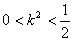 ……(13分)
……(13分)
∴ 直線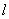 的斜率
的斜率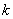 的取值范圍是
的取值范圍是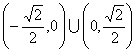 ……(14分)
……(14分)
(2)(文)若直線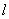 垂直于
垂直于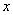 軸���,則
軸���,則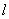 的方程為
的方程為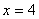 ,則
,則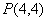 �,
�,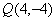 ,
,
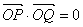 …………(8分)
…………(8分)
當(dāng)直線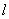 不垂直于
不垂直于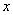 軸時����,設(shè)
軸時����,設(shè)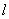 的方程為
的方程為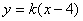 ,
,
由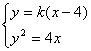 得
得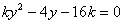 ……(10分)����,當(dāng)
……(10分)����,當(dāng) 時��,直線
時��,直線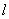 與拋物線總
與拋物線總
有兩個交點.設(shè)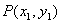 ��,
��,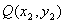 ���,則
���,則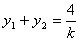 ,
,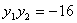 ……(12分)
……(12分)
∴ 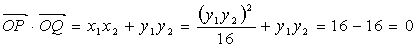
∴ 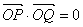 ……(14分)
……(14分)
21.(1)解方程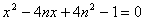 得
得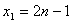 ����,
����,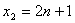 ……(1分)
……(1分)
∵ 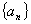 是遞增數(shù)列,∴
是遞增數(shù)列,∴ 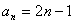 ����,
����,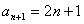 ,
,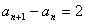 ……(3分)
……(3分)
∴ 數(shù)列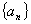 是等差數(shù)列�,其通項公式是
是等差數(shù)列�,其通項公式是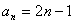 (
(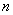 為正整數(shù))……(4分)
為正整數(shù))……(4分)
(2)當(dāng)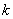 為正整數(shù)時,
為正整數(shù)時,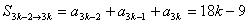
?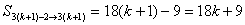 �����,∴
�����,∴ 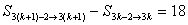 (常數(shù))
(常數(shù))
∴數(shù)列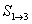 ����,
����,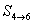 ���,
���,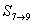 ,…��,
,…��,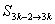 是等差數(shù)列……(9分)
是等差數(shù)列……(9分)
(3)(理)可以從多個方面加以推廣.對一般的以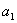 為首項��,
為首項��,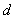 為公差的等差數(shù)列���,
為公差的等差數(shù)列���,
如照抄(2)中的問題(即三項之和)得2分�����,證明結(jié)論得3分,共得5分����;
如對(2)中的問題有所改變,如改為四項之和�,得3分,證明得3分��,共6分��;
如對(2)中的問題有所創(chuàng)新��,如:“對于任意給定的正整數(shù) ,判斷數(shù)列
,判斷數(shù)列
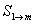 �����,
�����,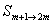 ���,……�,
���,……�,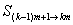 的類型”���,得4分���,證明結(jié)論得3分,共7分.
的類型”���,得4分���,證明結(jié)論得3分,共7分.
(3)(文)提出具體的若干項的問題的�,如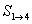 ,
,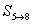 �����,……��,
�����,……��,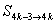 的�,得3分,
的�,得3分,
判斷結(jié)論得3分�����,共6分;
如對(2)中的問題有所創(chuàng)新�����,如:“對于任意給定的正整數(shù) ��,判斷數(shù)列
��,判斷數(shù)列
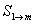 ��,
��,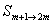 ����,……,
����,……,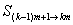 的類型”�����,得4分�,證明結(jié)論得3分�����,共7分.
的類型”�����,得4分�,證明結(jié)論得3分�����,共7分.
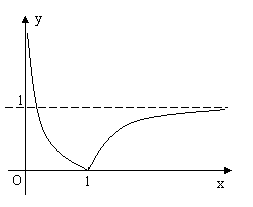
?22.(1)圖象如右圖所示.……(3分)
單調(diào)遞減區(qū)間: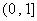 ����;……(4分)
����;……(4分)
單調(diào)遞增區(qū)間: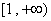 ……(5分)
……(5分)
(2)(理)由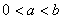 �,
�,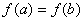
及函數(shù)的單調(diào)性知�,
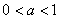 ,
,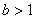 ����,……(7分)
����,……(7分)
∴ 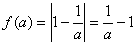 ,
,
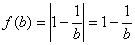 ����,由
����,由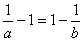
得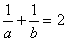 ,
,
∴ 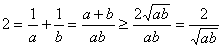 ��,∴
��,∴ 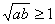 ���,即
���,即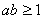 ……(10分)
……(10分)
(2)(文)由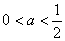 ���,
���,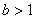
得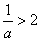 ,
,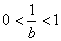 �����,……(7分)
�����,……(7分)
于是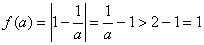 ���,
���,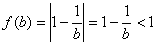 ……(9分)
……(9分)
∴ 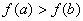 ……(10分)
……(10分)
(3)(理)當(dāng)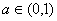 ����,
����,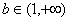 時,
時,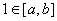 ����,而
����,而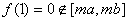 ,矛盾.
,矛盾.
∴ 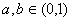 或
或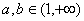 ……(12分)
……(12分)
當(dāng)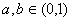 時�,由
時�,由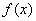 是減函數(shù)知,
是減函數(shù)知,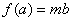 ����,
����, ,
,
即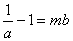 ��,
��,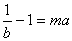 ��,得
��,得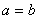 �����,舍去.……(14分)
�����,舍去.……(14分)
當(dāng)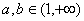 時���,由
時���,由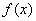 是增函數(shù)知�����,
是增函數(shù)知�����,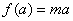 �,
�,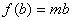 �,
�,
即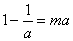 ,
,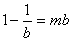 �����,∴
�����,∴ 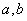 是方程
是方程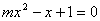 的兩個不相等實根�,且這
的兩個不相等實根�,且這
兩根均大于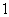 .
.
∴ △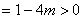 且
且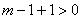 ,
,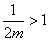 ��,解得
��,解得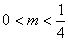 ……(17分)
……(17分)
∴ 實數(shù) 的取值范圍是
的取值范圍是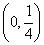 …(18分)
…(18分)
(3)(文)當(dāng)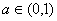 ��,
��,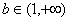 時��,
時��,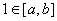 �,而
�,而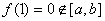 ,矛盾.
,矛盾.
∴ 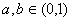 或
或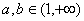 ……(12分)
……(12分)
當(dāng)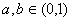 時��,
時��,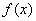 是減函數(shù)��,于是有
是減函數(shù)��,于是有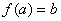 ,
,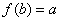 ����,
����,
即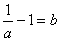 ,
,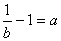 ����,得
����,得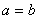 ,舍去.……(14分)
,舍去.……(14分)
當(dāng)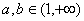 時�,由
時�,由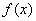 是增函數(shù)知,
是增函數(shù)知,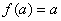 �,
�,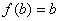 ,
,
即 ����,
����,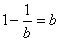 ,∴
,∴ 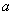 ����,
����,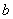 是方程
是方程 的兩根,但方程
的兩根,但方程
沒有實根.即實數(shù)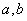 也不存在.……(17分)
也不存在.……(17分)
∴ 不存在這樣的實數(shù)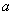 �,
�,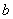 (
(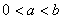 ),使得函數(shù)
),使得函數(shù)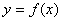 在
在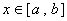 上的值域也
上的值域也
是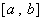 .……(18分)
.……(18分)
獲得更多試題及答案��,歡迎聯(lián)系微信公眾號:ygjjcom
